Use of the Technique of Infinitesimal Transformations of groups for finding the similarity solutions of Heat Equation

 Abstract
The diffusion (heat)equation is derived using thermal energy of a body with uniform properties, Fourier’s law of heat transfer and the law of conservation energy. It is solved using the technique of infinitesimal transformations of groups. Using this technique, the similarity solution is obtained for one dimentional diffusion(heat) equation with constant diffusion coefficient. The solution is obtained in the form of Hermite polynomial which is well suited for meaningful interpretation of the response of the physical problem.

Keywords: Diffusion, Infinitesimal transformation, Similarity Solution, Hermite polynomial.Introduction

The diffusion is one of the transport process that occur in nature. Diffusion is as central to our daily lives. The diffusion plays  a key role in many process as diverse as intermixing of gases and liquids, permeation of atoms or molecules through membranes, evaporation of liquids, drying of timbers, doping silicon wafers to make  semiconductor devices, transport of thermal neutrons in nuclear power reactors and heat transform. In this paper we review the heat equation. The heat or diffusion equation describes the heat transport due to combined effect of diffusion and convection in a medium. It is a partial differential equation of parabolic type, derived on the principle of conservation of mass using Fick’s law. There are many researchers, who have discussed about this topic from different aspects, such as, for example, A.J.Janavicius and S.Turskiene[1] have obtained analytical solution of nonlinear diffusion equation; Nataliya M. Ivanova[2] has derived the exact solution of diffusion-convection equation. The systematical investigation of invariant solutions of different diffusion equation was started by the case of linear heat equation. (Miller W.[3] and Olver P.[4]). The infinite series solution of the diffusion equations are obtained by Carslow and Jaeger[5]; Crank[6] and others. In the mathematical theory of diffusion, the diffusion coefficient can be taken as constant in some cases, such as diffusion in dilute solution. In other cases, such as diffusion in high polymers, the diffusion coefficient depends on the concentrations of diffusing substance[6]. This paper presents similarity solution of one dimentional diffusion equation with constant diffusion coefficient. This solution is obtained[9] by using a technique of infinitesimal transformations of groups. The solution obtained is physically consistant with results of earlier researchers[8] and which is more classical than other results obtained by the earlier researchers.

Physical derivation

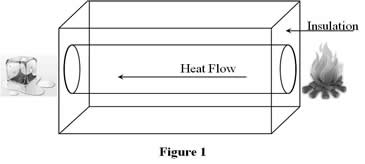
Here there are three physical principles can be used:

1. Heat (or thermal) energy of a body with uniform properties:

Heat energy = cmu,
where m is the body mass, u is the temperature, c is the specific heat, units [c]= L²T⁻²U⁻¹ (basic units are M mass, L length, T time, U temperature). c is the energy required to raise a unit mass of the substance 1 unit in temperature.
2. Fourier’s law of heat transfer: Rate of heat transfer proportional to negative temperature gradient,

.....(1)

where k₀ is the thermal conductivity, In other words, heat is transferred from areas of high temperature to low temperature.
3. Conservation of energy:
Consider a uniform rod of length l with non-uniform temperature lying on the x-axis from x = 0 to x = L. By uniform rod, we mean the density ρ, specific heat c, thermal conductivity k₀, cross-sectional area A are ALL constant. Assume the sides of the rod are insulated and only the ends may be exposed. Also assume there is no heat source within the rod. Consider an arbitrary thin segment of the rod thin slice of the rod of width Δx between x and x +Δx. The slice is so thin that the temperature throughout it is u(x, t). (Figure 2)

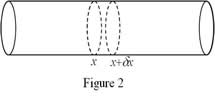
Thus,
Heat energy of segment = c × ρAΔx × u = cρAΔxu(x, t).
By conservation of energy,
(change of heat energy of segment in time Δt) = (heat in from left boundary) – (heat out from right boundary)
From Fourier’s Law (1),

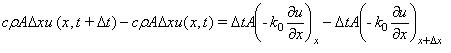
Rearranging yields (recall ρ, c, A, k₀ are constant),

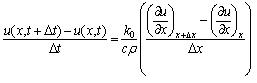
Taking the limit Δt, Δx → 0 gives the Heat Equation,

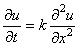.........(2)

where constant.      ........ (3)

Since the slice was chosen arbitrarily, the Heat Equation (2) applies throughout the rod.

Similarity Solution

We consider all possible groups of infinitesimal transformation that will reduce the diffusion equation (2) to an ordinary differential equation. In applying such a technique to a given differential equation, it may turn out that for some or all of the groups other than the linear and spiral groups, the boundary condition cannot be transformed although the partial differential equation can be transformed into an ordinary differential equation. For such cases, we are at least assured that the groups of infinitesimal transformations that remain are the groups possible for the given boundary value problems.

A similarity analysis of the diffusion equation from this point of view is apparently not covered in the literature. The one-dimensional form of the diffusion equation in rectangular coordinate is chosen because of its simplicity. Extension of analyses to equations expressed in other coordinates can readily be made.

Consider the diffusion equation

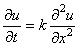.........(4)

Where k is constant. On which an infinitesimal transformation is to be made on the dependent and independent variables and derivatives of the dependent variable with respect to the independent variable. The infinitesimal transformations are

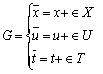.........(5)

Where generaters X, T and U are functions of x, t and u. Invarience of equation (1) under (2)  gives,

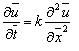..........(6)

Applying transformations (5) into the (6) we get the group of infinitesimal transformation explicitely is

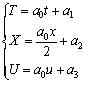.........(7)

Thus, the characteristic equations are

........(8)

From these we can have the similarity variable

.......(9)

also we have .......(10)

Let us discuss two different cases:

Case(1): If , then we get the ordinary differential equation,

.........(11)

This is a second order nonlinear ordinary differential equation and the solution of this equation is given by [9],

.........(12)

...........(13)

where c₁ and c₂ are constants and H_n(x) is n^th Hermite polynomial in x.

Case(2): If , then we get,

.......(14)

Which is also second order nonlinear ordinary differential equation and similar to the equation (11), and the solution is,

........(15)

..........(16)

where c₁ and c₂ are constants and H_n(x) is n^th Hermite polynomial in x.

Conclusion

I have discussed here a specific problem of one dimentional diffusion equation under certain assumptions and obtained the similarity solution using the technique of a groups of  infinitesimal transformations. I have expressed the solution in the form of Hermite polynomial which is well suited for meaningful interpretation of the response of the physical problem. The numerical illustrations, although not discussed here due to our restrictive interest in the similarity study.

REFERENCES :

1. A. J. Janavicius and S. Turskiene, Analytical solution of nonlinear diffusion equation in two dimentional surface, Acta physica polonica A, Vol 108 No. 6, 2005.
2. Nataliya M. Ivanova, exact solution of diffusion-convection equation; Dynamics of PDE; Vol 5 No. 2; 139-171; (2008).
3. Miller W.: Symmetry and separation of variable,reading, Addition-wesley, (1977).
4. Olver P.: Applications of Lie groups of differential equations, New York,Springer-Verlag, (1986)
5. H. S. Carslow and J. C. Jaeger: Conduction of heat in solids; Chap. 3, 2nd ed. Clarendon press, Oxford.(1959)
6. J. Crank: The Mathematics of Diffusion, Chap. 4, 2nd ed, Clarendon press, Oxford.(1975)
7. H. B. Fischer, E. J. List, R. C. Y. Koh, J. Imberger and N. A. Brooks:Mixing in inland and coastal waters, Academic press, Inc., NY (1979).
8. K. J. Chauhan and Dr. D. M. Patel: The similarity solution of the diffusion equation using the technique of infinitesimal transformations of groups, Journal of Science, Govt. of Gujarat, Gandhinagar, Issue 2, ISSN 2320-0006.
9. G. M. Murphy:Ordinary differential equations and their solutions, Van Nostrand reinhold company, NY.(1960),P 323.